




Leila Issa
I am interested in modelling fluids from the mirco to the macro scale.
On the macro scale, I am interested in modelling pollutant transport in the ocean.
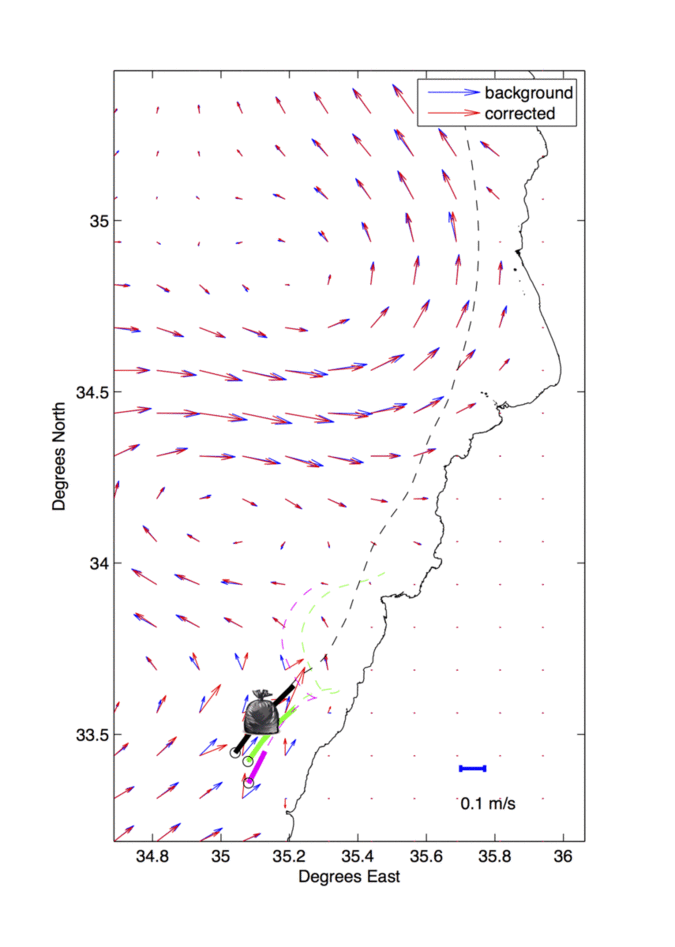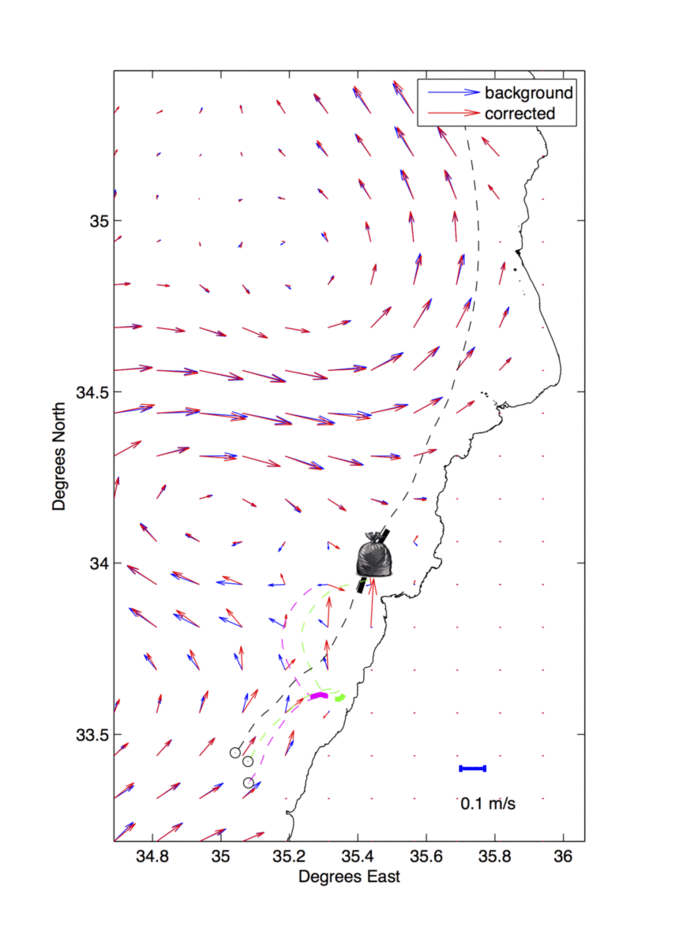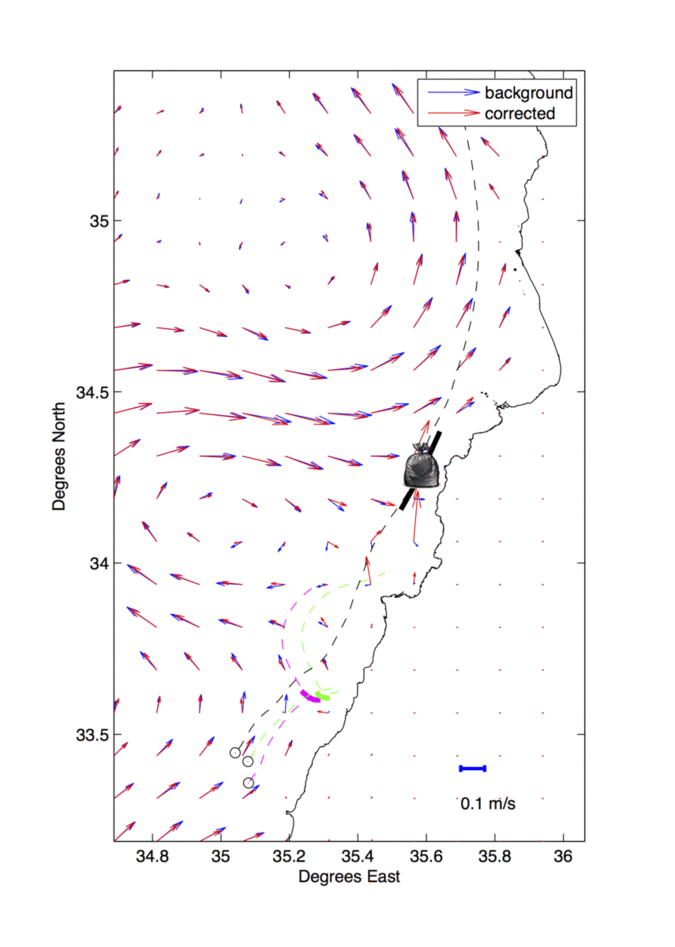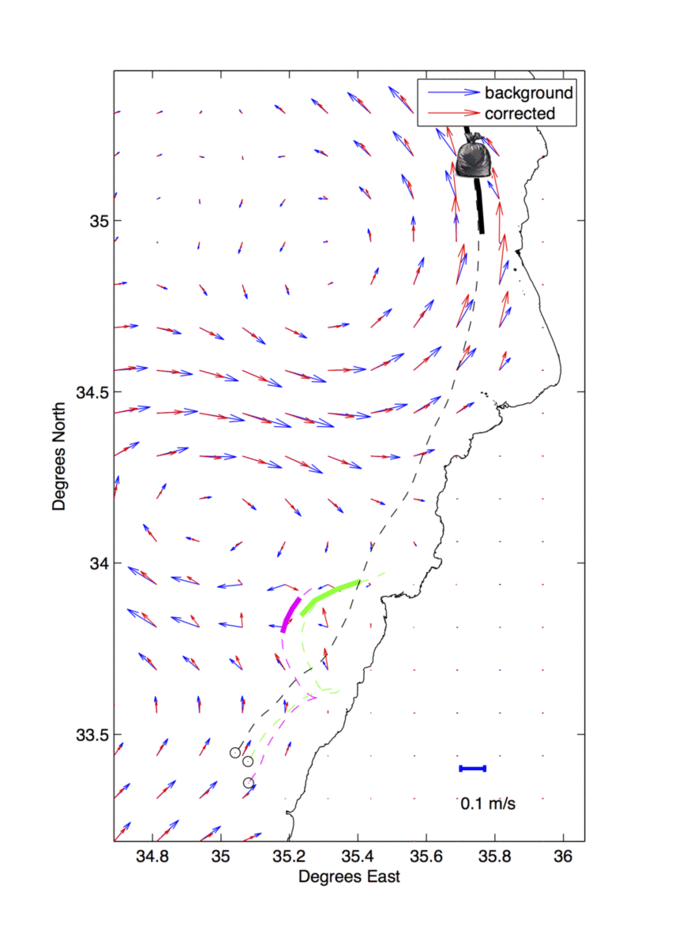
For this purpose, an accurate estimation of mesoscale to sub-mesoscale surface dynamics is critical. For instance this estimation can be used in studying pollutant dispersion emanating from heavily populated coastal areas, such as those of Lebanon. A good knowledge of the surface velocity field can be challenging, specially when direct observations are relatively sparse.
Within the context of the AltiFloat project, done in collaboration with LOCEAN laboratory at Paris VI and the lebanese CNRS, we proposed a near real time 3D-Var assimilation algorithm that provides continuous corrections to the geostrophic field, known to be inaccurate near the coast.
The figure on the right demonstrates the result of assimilating three drifters trajectories, launched from the south of Beirut, with altimetry based geostrophic currents and wind speed data, near the Lebanese coast. The surface velocity field starts from the altimetric one (blue) and is continuously corrected (red) as more drifter and wind data are available.
This research was featured in QS WOWNEWS magazine, Issue 28.
I am also collaborating with the American University of Beirut and King Abdullah University of Science and Technology on Lagrangian tracking in stochastic flows fields within a sequential ensemble data assimilation framework. This problem is challenging due to the exponential growth in the number of particles arising from describing the behavior of velocity over time as a set of possible combinations of the different realizations, before and after each assimilation cycle.
We proposed an efficient algorithm for forward and backward tracking of passive particles in stochastic flow-fields while capping the number of particles to a desired maximum. The mechanism uses an adaptive binning procedure, while conserving the zeroth, first and second moments of probability (total probability, mean position, and variance).
The figure on the right shows probability maps (using an ensemble flow field of 100% the standard deviation of the initial dataset) after 27 days of releasing the tracer at the source (black square) . The number of particles is capped to 50 million and the time step of 4 hours.
Red square: location of the highest probability at the end of forward tracking.


On the micro scale, my recent research activities involve development and solution of asymptotic-based models for unsteady incompressible pressure-driven micro-flows in long channels of variable cross-section. These semi-analytic models are typically two orders of magnitude faster than computational fluid dynamics (CFD) simulations, rendering them an essential tool for exploring design parameter spaces. This work has important applications in design of microfluidic devices and in modelling of bio-flows. Mircofluidic devices such as uTAS and lab-on-chip integrate one or several laboratory functions on a single chip of only a few square millimeters. Bioflows applications include modeling of gases transport in the airways and blood transport in the complex network of blood vessels.
The pictures below show the effect of unsteadiness on the flow in a variable circular channel whose profile is depicted in the figure above. On the left, we see snapshots of the axial and radial velocities at different locations in the channel. We observe the impact of the viscous effect on the flow reversal, which is seen as a delay in reversal of the velocity near the wall, when compared to the velocity at the center-line. This delay is expected to increase as inertia effects grow. The flow reversal can also be seen in the corresponding color maps of the velocity components shown on the right.
An important aspect of unsteadiness is the incurred increase in the computational cost in CFD simulations. For this scenario, the computational cost of the reduced order model is two orders of magnitude smaller (∼500 times) than the CFD simulation.
This research was recently featured in the July issue of Applied Mathematical Modelling.

